Optimizing Customer Order Fulfillment Costs: A Practical Approach Using AI
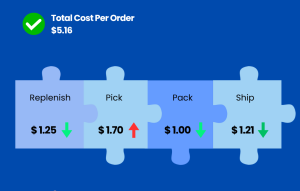
In today’s dynamic supply chain and logistics industry, keeping costs under control is crucial to achieving competitive advantage. Fulfillment centers deal with various costs like labor, shipping, and handling, which require careful balancing to ensure customers receive their products on time without inflating operational expenses. This post dives into how you can optimize these costs using mixed integer programming, specifically with the help of Google’s OR-Tools.
The Shipping Cost Challenge
When processing customer orders, especially when products are distributed across multiple facilities, the decision on how much to ship from each facility can significantly impact costs. Shipping from the wrong facility, or using an expedited delivery when it’s not needed, can lead to inflated costs that eat into profit margins.
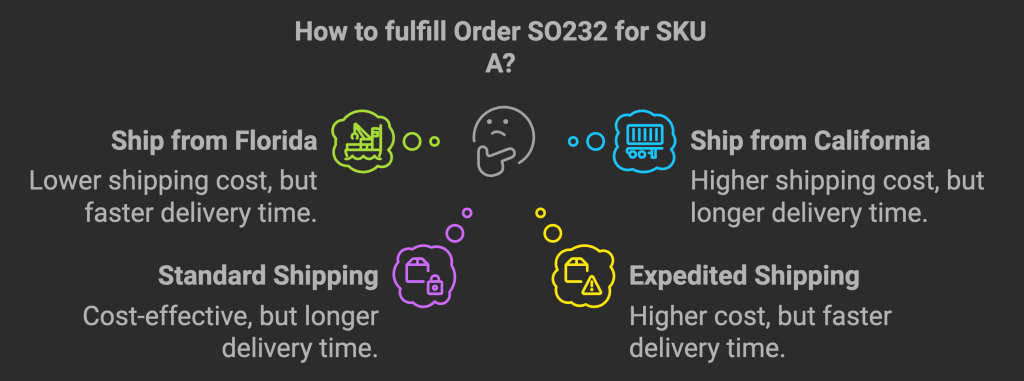
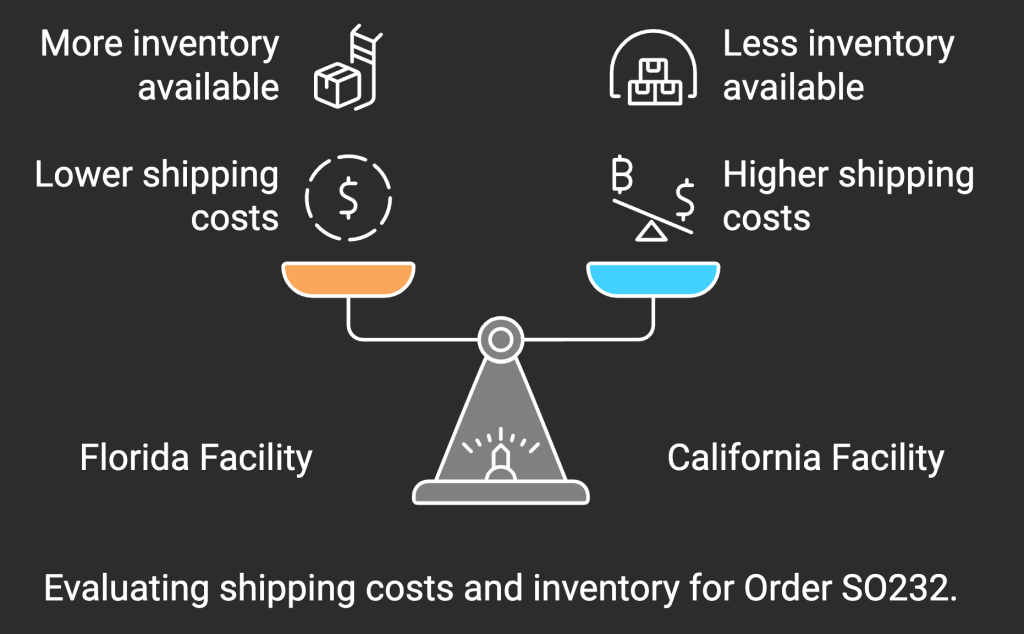
For example, consider the case of Order SO232, which involves a product (SKU A) that must be shipped to a customer in Georgia. The order needs 13 units, and we have two facilities, one in Florida and one in California, each with different inventory levels, shipping costs, and delivery timelines.
The challenge is to determine:
How many units should be shipped from each facility?
Which shipping option (standard or expedited) should be selected?
How can labor and shipping costs be minimized?
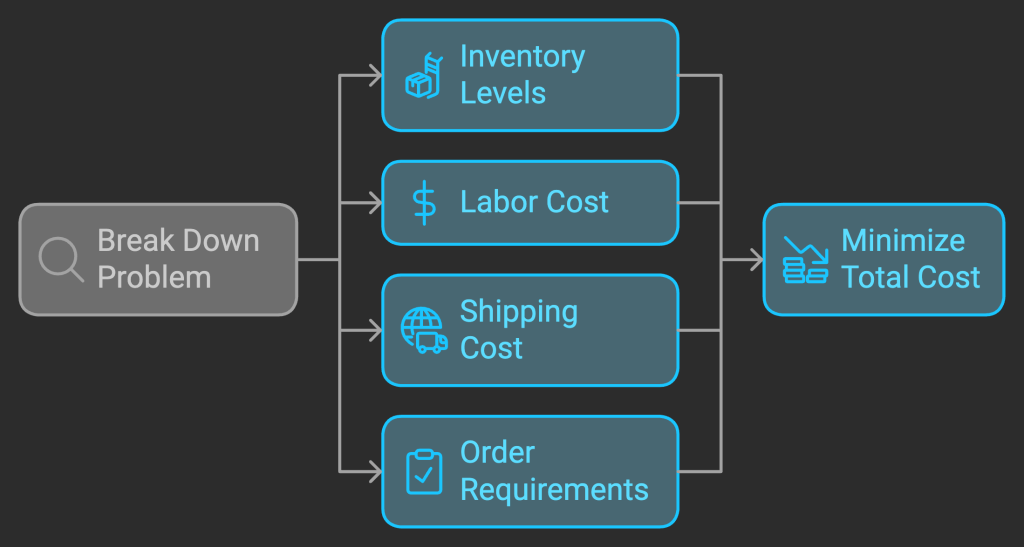
Breaking Down the Problem
To solve this, we need to consider multiple factors:
Inventory Levels: How many units are available at each facility.
Labor Cost: Cost per unit for packing and preparing products for shipment.
Shipping Cost: Cost per pound for various shipping methods (e.g., 1-Day, 2-Day, 5-Day delivery).
Order Requirements: The total quantity needed and the desired delivery date.
Our goal is to minimize the total cost, which includes both labor costs and shipping costs, while ensuring the product is delivered on time.
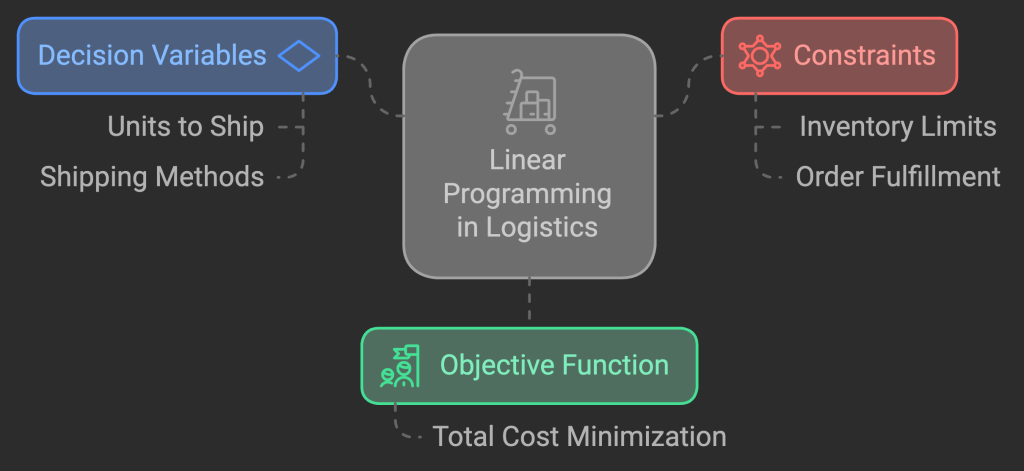
How Mixed Integer Programming Helps
Mixed integer programming (LP) is a mathematical approach used to achieve the best outcome in a given mathematical model, where the objective is to either minimize or maximize a particular value. In this case, we want to minimize fulfillment costs while meeting inventory and shipping constraints.
Using LP, we can create a model where:
Decision variables represent the number of units to ship from each facility using each available shipping method.
The objective function represents the total cost we want to minimize.
Constraints ensure we don’t exceed inventory limits and that we fulfill the total order requirement.
Using Google OR-Tools for Fulfillment Optimization
Google OR-Tools is a powerful open-source optimization toolkit that can solve a variety of mathematical optimization problems, including mixed integer programming. Here’s how we approached solving the fulfillment cost optimization for Order SO232 using mixed integer programming.
Defining the Variables
For our example:
We have two facilities: Florida (FL_FAC) and California (CA_FAC).
There are multiple shipping options available from each facility (e.g., 1-Day, 2-Day, 5-Day).
Each shipping option has an associated shipping rate based on the weight of the product.
We define a decision variable for each possible shipping method:
For instance, FL_FAC_SO232_A_10_Day represents the number of units of SKU A shipped from the Florida facility using the 10-Day shipping method.
Objective Function: Minimizing Costs
The objective function in our model represents the total cost, which includes both labor and shipping costs.
The labor cost per unit is $0.10, and the shipping cost is determined by multiplying the per-pound rate by the weight of the product (0.15 lb per unit for SKU A). For each shipping option from each facility, the total cost per unit shipped is calculated as:
Labor Cost ($0.10) + Shipping Cost (Rate per lb * 0.15 lb).
For example:
If we ship SKU A using the 10-Day shipping method from the Florida facility (FL_FAC), which costs $5 per pound, the total cost per unit is: 0.10+(5×0.15)=0.850.10 + (5 \times 0.15) = 0.850.10+(5×0.15)=0.85
This cost calculation is repeated for each facility and shipping method, creating an objective function that can be minimized.
Constraints
In order to achieve a feasible and optimal solution, several constraints must be defined:
Total Order Quantity Constraint:
The total quantity shipped from all facilities must be equal to the order requirement, which is 13 units for Order SO232.
This ensures that no more or less than the required amount is shipped.
Inventory Constraints:
Facility-Specific Inventory Constraints ensure that the amount shipped from each facility does not exceed the available inventory at that facility.
For example:
The Florida facility (FL_FAC) has 12 units available, so any combination of shipping options from Florida cannot exceed this limit.
Non-Negative Constraints:
All decision variables must be greater than or equal to zero, meaning that negative shipment quantities are not allowed.
The Solution
After running the above JSON through Google OR-Tools, the solver will determine:
The optimal number of units to ship from each facility.
Which shipping method should be used to minimize the total cost.
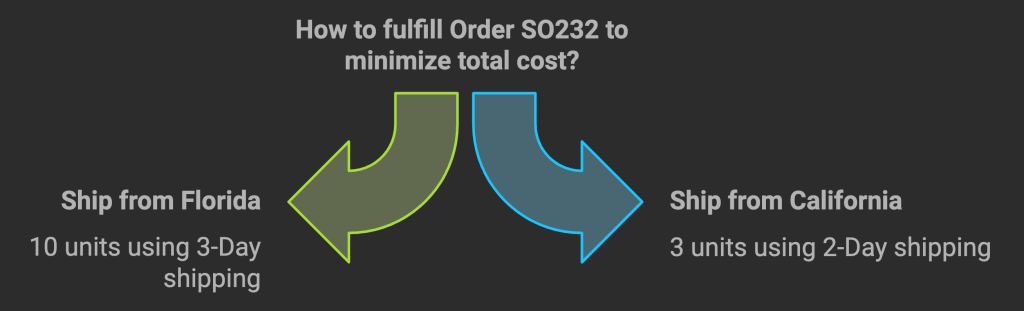
For Order SO232, the solver may find, for example, that 10 units should be shipped from the Florida facility using the 10-Day shipping method, and 3 units should be shipped from California using the 2-Day shipping method. This solution minimizes the total fulfillment cost while respecting inventory constraints and order requirements.
Conclusion
Fulfillment cost optimization using mixed integer programming provides a structured approach to minimize the total cost of labor and shipping while meeting customer demand effectively. By using tools like Google OR-Tools, businesses can automate and optimize decisions about how much to ship from each facility and which shipping options to choose.
The benefits of applying mixed integer programming to fulfillment challenges include:
Cost Savings: Minimizing labor and shipping costs while still meeting customer expectations.
Improved Efficiency: Ensuring that inventory levels are utilized effectively and shipping methods are chosen based on cost-effectiveness.
Scalable Solutions: This approach can easily be extended to more complex scenarios with multiple products, facilities, and diverse customer requirements.
For any business managing fulfillment operations, incorporating an optimization model such as this can help ensure cost-effective decision-making and maintain a competitive edge in the supply chain landscape.
Ready to transform your fulfillment strategy?
Discover how ProfitOps.ai can help you optimize your logistics, reduce costs, and streamline your order fulfillment processes. Book a demo with our experts today and see how our cutting-edge solutions can take your fulfillment operations to the next level!
Shravan Talupula
Founder, ProfitOps